Član
- Učlanjen(a)
- 03.10.2011
- Poruka
- 58
Prepostavka-Dva i više srki množenja mogu se skraćeno napisati , znak = može biti >(<)
Proces:
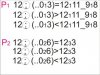
P[SUB]1[/SUB]5×(s.4.ß) 5=¤1[SUB]f2[/SUB](3[SUB]2[/SUB]1)1[SUB]f2[/SUB]¤_1
5×(s.4.ß)5>¤1[SUB]f2[/SUB](3[SUB]2[/SUB]1)1[SUB]f2[/SUB]¤_1
5×(s.4.ß)5<¤1[SUB]f2[/SUB](3[SUB]2[/SUB]1)(1)1[SUB]f2[/SUB]¤_1
P[SUB]2[/SUB] 5×(.ß3)5=¤1[SUB]f2[/SUB](1[SUB]2[/SUB]3)1[SUB]f2[/SUB](1)1¤
5×(.ß3)5>¤1[SUB]f2[/SUB](1[SUB]2[/SUB]3)1[SUB]f2[/SUB](1)1¤
5×(.ß3)5<¤1[SUB]f2[/SUB](1[SUB]2[/SUB]3)1[SUB]f2[/SUB](1)1¤
...
[S[SUB]30[/SUB]]-funkcija srki množenje - jednačina , nejednačina
SM-Ne poznaje funkciju srki množenje
Proces:
P[SUB]1[/SUB]5×(s.4.ß) 5=¤1[SUB]f2[/SUB](3[SUB]2[/SUB]1)1[SUB]f2[/SUB]¤_1
5×(s.4.ß)5>¤1[SUB]f2[/SUB](3[SUB]2[/SUB]1)1[SUB]f2[/SUB]¤_1
5×(s.4.ß)5<¤1[SUB]f2[/SUB](3[SUB]2[/SUB]1)(1)1[SUB]f2[/SUB]¤_1
P[SUB]2[/SUB] 5×(.ß3)5=¤1[SUB]f2[/SUB](1[SUB]2[/SUB]3)1[SUB]f2[/SUB](1)1¤
5×(.ß3)5>¤1[SUB]f2[/SUB](1[SUB]2[/SUB]3)1[SUB]f2[/SUB](1)1¤
5×(.ß3)5<¤1[SUB]f2[/SUB](1[SUB]2[/SUB]3)1[SUB]f2[/SUB](1)1¤
...
[S[SUB]30[/SUB]]-funkcija srki množenje - jednačina , nejednačina
SM-Ne poznaje funkciju srki množenje