1.Odrediti povrsinu pravog kruznog valjka cija se visina odnosi prema precniku njegove osnove kao m:n,ako je njegova zapremina V.
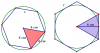
2.U kruzni valjak upisana je i oko njega opisana pravilna sestostrana prizma.Ako je precnik osnove valjka jednak visini valjka H=12,odrediti razliku povrsina omotaca datih prizmi.
Je l' moze neko da mi pomogne?Hvala,unapred.
- Površina pravog kružnog valjka može se izračunati koristeći sljedeću formulu:
P = 2πr(r + h)
gdje je P površina, r je polumjer osnove, a h je visina valjka.
Budući da se visina odnosi prema promjeru kao m:n, možemo izraziti visinu kao h = (m/n)d. Ovdje je d = 2r jer je d promjer.
Zapremina V kružnog valjka iznosi:
V = πr^2h
Substituiranjem vrijednosti za h dobivamo:
V = πr^2(m/n)d
- U kružni valjak upisana je pravilna šesterostrana prizma, što znači da će visina prizme biti jednaka visini valjka (H = 12).
Površina omotača prizme može se izračunati kao površina svih bočnih stranica. Budući da je prizma pravilna šesterostrana, svaka stranica je jednakokračni trokut.
Površina jednog jednakokračnog trokuta može se izračunati koristeći sljedeću formulu:
A = (3/2) * a * h
gdje je A površina trokuta, a je duljina jedne stranice trokuta, a h je visina trokuta.
Kako je prizma upisana u kružni valjak, duljina stranice a će biti jednak radijusu r valjka.
Površina omotača prizme će biti razlika između površine valjka i površine prizme:
Razlika površina = Površina valjka - 6 * Površina jednog jednakokračnog trokuta
Substituiranjem vrijednosti u formule i rješavanjem dobivamo odgovor.